What is a finite number? In the realm of mathematics, finite numbers play a crucial role in various fields such as algebra, calculus, and statistics. A finite number is defined as any number that is not infinite; it has a definite value that can be quantified. The concept of finite numbers is fundamental for anyone looking to understand mathematical principles and applications, making it an essential topic for students and enthusiasts alike.
In this article, we will explore the definition of finite numbers, their properties, and their significance in mathematics. We will delve into various examples and applications of finite numbers to provide a well-rounded understanding of this concept. Whether you are a student trying to grasp the basics or a professional seeking to refresh your knowledge, this guide aims to illuminate the topic of finite numbers.
By the end of this article, you will not only comprehend what finite numbers are but also appreciate their importance in everyday mathematical applications. Let’s embark on this journey into the world of finite numbers!
Table of Contents
- Definition of Finite Numbers
- Properties of Finite Numbers
- Examples of Finite Numbers
- Applications of Finite Numbers
- Finite Numbers vs. Infinite Numbers
- Importance of Finite Numbers in Mathematics
- Finite Numbers in Statistics
- Conclusion
Definition of Finite Numbers
A finite number can be described as a real number that is not infinite. It has a specific, countable quantity and can be expressed in various forms, such as integers, rational numbers, and real numbers. The key characteristic of finite numbers is that they can be measured, counted, or expressed in numerical terms.
Characteristics of Finite Numbers
- Definiteness: Finite numbers have a specific value.
- Countability: They can be counted or measured.
- Representability: Finite numbers can be expressed in decimal or fractional forms.
Properties of Finite Numbers
Finite numbers possess several essential properties that distinguish them from other types of numbers. Understanding these properties is crucial for applying finite numbers in various mathematical contexts. Here are some key properties:
1. Additive Property
The sum of two finite numbers is always a finite number. For example, 3 + 5 = 8 is a finite number.
2. Multiplicative Property
The product of two finite numbers is also a finite number. For instance, 4 × 6 = 24, which is finite.
3. Order
Finite numbers can be ordered. For example, in the set of finite numbers, 2 < 5 < 10.
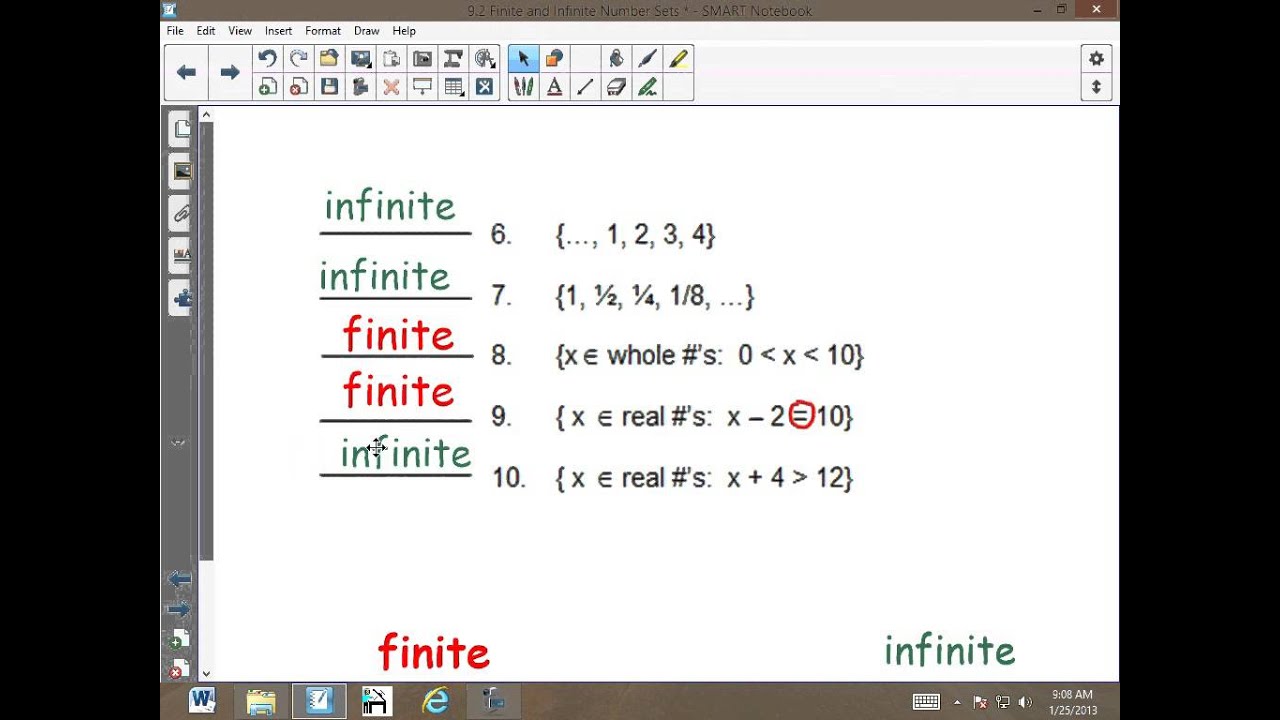
Examples of Finite Numbers
To better understand finite numbers, let’s look at some examples:
- Integers: -3, 0, 5, 10
- Rational numbers: 1/2, 3/4, 7/8
- Real numbers: 2.5, -1.75, 0.333
Applications of Finite Numbers
Finite numbers are used in various applications across different fields, including:
- Statistics: Finite numbers are used to represent data sets, averages, and probabilities.
- Finance: Finite numbers are crucial for calculating interest rates, loan amounts, and investments.
- Engineering: Finite numbers are used in measurements, calculations, and modeling.
Finite Numbers vs. Infinite Numbers
Understanding the difference between finite and infinite numbers is essential in mathematics. While finite numbers have specific values, infinite numbers represent quantities that are unbounded and cannot be counted. For example, the concept of infinity (∞) is used to describe something that has no end. In contrast, finite numbers are confined to a specific range.
Importance of Finite Numbers in Mathematics
Finite numbers are the building blocks of mathematics. They are essential for computations, problem-solving, and theoretical applications. Without finite numbers, many mathematical concepts and principles would not be possible. They provide a foundation for understanding more complex mathematical ideas, making them indispensable in the study of mathematics.
Finite Numbers in Statistics
In statistics, finite numbers are used to represent data points, calculate averages, and analyze trends. They allow statisticians to make informed decisions based on quantifiable data. Some key applications include:
- Data analysis: Utilizing finite numbers to interpret data sets.
- Probability: Calculating the likelihood of events using finite numbers.
- Statistical modeling: Applying finite numbers to create models that predict outcomes.
Conclusion
In summary, finite numbers are a fundamental concept in mathematics with various applications across different fields. They are defined by their specific, countable values and possess properties that allow for mathematical operations. Understanding finite numbers is crucial for anyone looking to delve deeper into mathematics or utilize mathematical principles in real-world situations. We encourage you to share this article, leave comments, and explore more about the fascinating world of mathematics!
Call to Action
If you found this article helpful, consider sharing it with others who might benefit from understanding finite numbers. Also, feel free to explore other articles on our site for more insights into mathematics and its applications!
Thank you for reading, and we hope to see you again soon!